Motivation
This blog post is my note taken when studying Neural Oridinary Differential Equation (NeuralODE), which was proposed in Neural Ordinary Differential Equations. The goal of this note is to understand the formulation, some mathematical derivations, and some techincal difficulties encounter when implementing NeuralODE in JAX.
The entire learning process is quite fascinating and introduced me to some new mathematical concepts such as Euler-Lagrange equation, Continuous Lagrangian Multiplier. NeuralODE is a important entry point to Physics Informed Machine Learning and I struggled for quite sometime to understand. So I hope this post might save sometime for people who are also trying to understand NeuralODE.
NeuralODE
Formulation
Many systems can be written as a ODE’s initial value problem:
$$ \begin{equation} \begin{cases} \frac{d\mathbf{u}}{dt} = f(\mathbf{u}, t) \\ \mathbf{u}(t=0) = \mathbf{u}_0 \end{cases} \end{equation} $$
Where:
- \(\mathbf{u} \in \mathbb{R}^N\) describes the state of the system.
- \(\mathbf{u}(t)\) is the state of the system at time \(t\).
- \(f: \mathbb{R}^N \rightarrow \mathbb{R}^N\) is a dynamic function that characterizes the system. Which means, at any given state of the system, \(f\) tells us the rate of change for that state \(\frac{d\mathbf{u}}{dt}\).
When \(f\) is given, this system of equations can be solved by numerical methods such as Euler, Predictor Corrector Method, or RK45 (see my previous post on ODE Integrator).
NeuralODE solves the inverse problem, given some observations of the system state \(\{(\mathbf{u}_i, t_i)\}_{i=1\cdots N}\) (which can be irregularly sampled), find the dynamic function \(f\). NeuralODE parameterize \(f\) by a neural-network \(f_\theta\), where \(\theta \in \mathbb{R}^P\) is the set of parameters of the network. For simplicity, assume that we have only two observations at \(t=t_0\) and \(t=t_1\). NeuralODE’s prediction of the system state at \(t=t_1\) are given by:
$$ \begin{equation} \hat{\mathbf{u}}_1 = \mathbf{u}_0 + \int_{t_0}^{t_1}{f(\mathbf{u}, t;\theta)dt} \end{equation} $$
NeuralODE learns the parameter \(\theta\) by minimizing the difference between its prediction and groundtruth \(\mathbf{u}_1\):
$$ L(\hat{\mathbf{u}}_1, \mathbf{u}_1) = \text{MSE}(\mathbf{u}_1, \mathbf{\hat{u}}_1) $$
Finally, NeuralODE can be formulated as a constrained optimization problem:
$$ \begin{equation} \begin{aligned} & \min_\theta L(\hat{\mathbf{u}}_1, \mathbf{u}_1) \\ \text{such that: } & \frac{d\mathbf{u}}{dt} = f(\mathbf{u}, t;\theta)\quad \forall t_0\leq t \leq t_1 \end{aligned} \end{equation} $$
In order to solve the optimization problem in equation 3), we need to compute the sensitivity \(\frac{dL}{d\theta}\). The following sections will discuss the method of computing this quantity.
The forward sensitivity method
The forward sensitivity method is a straight forward method of computing \(\frac{dL}{d\theta}\):
$$ \begin{equation} \begin{aligned} \frac{dL}{d\theta} & = \frac{d}{d\theta} L(\mathbf{u}_1, \mathbf{\hat{u}}_1) \\ & = \underbrace{\frac{\partial L}{\partial \mathbf{\hat{u}}_1}}_{1\times N} \underbrace{\frac{d\mathbf{\hat{u}_1}}{d\theta}}_{N\times P} \end{aligned} \end{equation} $$
By differentiating both L.H.S and R.H.S of equation (1) with respect to \(\theta\), we have:
$$ \begin{equation} \begin{aligned} & \frac{d}{d\theta}(\frac{d\mathbf{u}}{dt}) = \frac{d}{d\theta}f(\mathbf{u}, t; \theta) \\ \iff & \frac{d}{dt}(\frac{d\mathbf{u}}{d\theta}) = \frac{\partial f}{\partial\theta} + \frac{\partial f}{\partial \mathbf{u}}\frac{d\mathbf{u}}{d\theta} \end{aligned} \end{equation} $$
Equation (5) gaves us a system of ODE initial value problem, which consists of \(N\times P\) individual ODE. We can see that by denoting \(A = \frac{d\mathbf{u}}{d\theta} \in \mathbb{R}^N\) is the Jacobian of state \(u\) with respect to parameter \(\theta\), \(A_{ij} = \frac{\partial u_i}{\partial\theta_j}\). To solve for \(\frac{d\mathbf{\hat{u}_1}}{d\theta}\), we solve \(N\times P\) individual ODE initial value problems with initial value is \(0\) (since \(\mathbf{u}_0\) doesn’t depend on \(\theta\)). The forward sensitivity method is computationally prohibited for the medium to large neural networks with thousands of parameters.
Equiped with this understanding, we can fully appreciate the adjoint sensitivity method, which is the key to understand NeuralODE.
The adjoint state method
We can write the constrainted optimization problem in equation (3) as unconstrainted one using continuous Lagrangian multiplier \(\lambda(t)\):
$$ \begin{equation} \begin{aligned} J(\mathbf{\hat{u}_1}, \lambda, \theta) = L(\mathbf{\hat{u}_1}) + \int_{t_0}^{t_1}{\lambda(t)(f - \frac{d\mathbf{u}}{dt} )dt} \end{aligned} \end{equation} $$
Where \(\lambda \in \mathbb{R}^N\) is the Lagrangian multiplier in the form of function of time. Take the derivative with respect to \(\theta\) for L.H.S and R.H.S in equation (6):
$$ \begin{equation} \begin{aligned} \frac{dJ}{d\theta} & = \frac{d}{d\theta}\bigg( L(\mathbf{\hat{u}_1}) + \int_{t_0}^{t_1}{\lambda(t)(f - \frac{d\mathbf{u}}{dt} )dt} \bigg) \\ & = \frac{d}{d\theta} L(\mathbf{\hat{u}_1}) + \int_{t_0}^{t_1}{ \frac{d}{d\theta} \lambda(f - \frac{d\mathbf{u}}{dt}) dt} \end{aligned} \end{equation} $$
Considering the first term in R.H.S of equation (7):
$$ \begin{equation} \begin{aligned} \frac{d}{d\theta}L(\mathbf{\hat{u}}_1) &= \frac{\partial L}{\partial \mathbf{\hat{u}_1}} \frac{d}{d\theta}( \mathbf{u}_0 + \int_{t_0}^{t_1}{f(\mathbf{u}, t; \theta)dt}) \\ & = \frac{\partial L}{\partial \mathbf{\hat{u}_1}} \int_{t_0}^{t_1}{ \bigg(\frac{\partial f}{\partial\theta} + \frac{\partial f}{\partial\mathbf{u}}\frac{d\mathbf{u}}{d\theta}\bigg)dt } \end{aligned} \end{equation} $$
And considering the second term of the R.H.S of equation (7):
$$ \begin{equation} \begin{aligned} & \int_{t_0}^{t_1}{ \frac{d}{d\theta}\lambda \bigg( f(\mathbf{u}, t;\theta) - \frac{d\mathbf{u}}{dt} \bigg) dt }\\ = & \int_{t_0}^{t_1}{ \lambda \bigg( \frac{\partial f}{\partial\theta} + \frac{\partial f}{\partial\mathbf{u}}\frac{d\mathbf{u}}{d\theta} - \frac{d}{d\theta}(\frac{d\mathbf{u}}{dt}) \bigg) dt }\\ = & \int_{t_0}^{t_1}{ \lambda \bigg( \frac{\partial f}{\partial\theta} + \frac{\partial f}{\partial\mathbf{u}}\frac{d\mathbf{u}}{d\theta} \bigg) dt } - \blue{ \int_{t_0}^{t_1}{ \lambda\frac{d}{d\theta}(\frac{d\mathbf{u}}{dt}) dt } } \end{aligned} \end{equation} $$
The final term in equation (9) can be evaluated by integration by parts after swapping the order of derivation:
$$ \begin{equation} \begin{aligned} & \int_{t_0}^{t_1}{ \lambda\frac{d}{d\theta}(\frac{d\mathbf{u}}{dt}) dt } \\ = & \int_{t_0}^{t_1}{ \lambda\frac{d}{dt}(\frac{d\mathbf{u}}{d\theta}) dt } \\ = & \bigg[\lambda \frac{d\mathbf{u}}{d\theta}\bigg]_{t_0}^{t_1} - \int_{t_0}^{t_1}{\frac{d\lambda}{dt}\frac{d\mathbf{u}}{d\theta}dt}\\ = & \lambda(t_1) \frac{d\mathbf{u}}{d\theta}\bigg\vert_{t_1} - \underbrace{\cancel{ \lambda(t_0)\frac{d\mathbf{u}}{d\theta}\bigg\vert_{t_0} }}_{=0} - \int_{t_0}^{t_1}{\frac{d\lambda}{dt}\frac{d\mathbf{u}}{d\theta}dt}\\ \end{aligned} \end{equation} $$
The second term cancelled out due to state \(u(t=0)\) doesn’t depend on \(\theta\). Replacing equation (10) back into equation (9):
$$ \begin{equation} \begin{aligned} & \int_{t_0}^{t_1}{ \frac{d}{d\theta}\lambda \bigg( f(\mathbf{u}, t;\theta) - \frac{d\mathbf{u}}{dt} \bigg) dt }\\ = & \int_{t_0}^{t_1}{ \lambda \bigg( \frac{\partial f}{\partial\theta} + \frac{\partial f}{\partial\mathbf{u}}\frac{d\mathbf{u}}{d\theta} + \frac{d\lambda}{dt}\frac{d\mathbf{u}}{d\theta} \bigg) dt } - \lambda(t_1) \frac{d\mathbf{u}}{d\theta}\bigg\vert_{t_1} \end{aligned} \end{equation} $$
Replacing result from equation (8) and (11) into equation (7):
$$ \begin{equation} \begin{aligned} \frac{dJ}{d\theta} &= \frac{\partial L}{\partial \mathbf{\hat{u}_1}} \int_{t_0}^{t_1}{ \bigg(\frac{\partial f}{\partial\theta} + \frac{\partial f}{\partial\mathbf{u}}\frac{d\mathbf{u}}{d\theta}\bigg)dt }\\ & + \int_{t_0}^{t_1}{ \lambda \bigg( \frac{\partial f}{\partial\theta} + \frac{\partial f}{\partial\mathbf{u}}\frac{d\mathbf{u}}{d\theta} + \frac{d\lambda}{dt}\frac{d\mathbf{u}}{d\theta} \bigg) dt }\\ & - \lambda(t_1) \frac{d\mathbf{u}}{d\theta}\bigg\vert_{t_1} \end{aligned} \end{equation} $$
Rearranging equation (12):
$$ \begin{equation} \begin{aligned} \frac{dJ}{d\theta} &= \int_{t_0}^{t_1}{ \big(\frac{\partial L}{\partial\mathbf{\hat{u}}_1} + \lambda\big)\frac{\partial f}{\partial\theta}dt }\\ & + \int_{t_0}^{t_1}{ \big( \frac{\partial L}{\partial\mathbf{\hat{u}}_1}\frac{\partial f}{\partial\mathbf{u}} + \lambda \frac{\partial f}{\partial\mathbf{u}} + \frac{d\lambda}{dt} \big)\frac{d\mathbf{u}}{d\theta} }\\ & - \lambda(t_1) \frac{d\mathbf{u}}{d\theta}\bigg\vert_{t_1} \end{aligned} \end{equation} $$
From the forward sensitivity method we know that \(\frac{d\mathbf{u}}{d\theta}\) is prohibitively expensive, we can choose the Lagrangian \(\lambda\) such that the last two terms in equation (13) vanish. Specifically:
$$ \begin{equation} \begin{aligned} & \begin{cases} \frac{\partial L}{\partial\mathbf{\hat{u}}_1}\frac{\partial f}{\partial\mathbf{u}} + \lambda \frac{\partial f}{\partial\mathbf{u}} + \frac{d\lambda}{dt} = 0 \\ \lambda(t_1) = 0 \end{cases} \\ \iff & \begin{cases} \frac{d\lambda}{dt} = -\big(\frac{\partial L}{\partial\mathbf{\hat{u}}_1} + \lambda\big) \frac{\partial f}{\partial\mathbf{u}}\\ \lambda(t_1) = 0 \end{cases} \end{aligned} \end{equation} $$
Denoting \(\mathbf{a}(t)=\lambda + \frac{\partial L}{\partial\mathbf{\hat{u}_1}}\), equation (14) became:
$$ \begin{equation} \begin{aligned} \begin{cases} \frac{d\mathbf{a}}{dt} = -\mathbf{a}(t)\frac{\partial f}{\partial \mathbf{u}}\\ \mathbf{a}(t_1) = \frac{\partial L}{\partial\mathbf{\hat{u}}_1} \end{cases} \end{aligned} \end{equation} $$
Equation (15) is a ODE terminal value problem, which can be solved by any ODE solver. The sensitivity \(\frac{dJ}{d\theta}\) in equation (13) became:
$$ \begin{equation} \frac{dJ}{d\theta} = \int_{t_0}^{t_1}{\mathbf{a}(t)\frac{\partial f}{\partial \theta}dt} \end{equation} $$
\(\mathbf{a}(t)\) is exactly the adjoint state that mentioned in the original paper. In the paper, the authors went with alternative proof using Taylor Expansion.
Summary strategy of computing the sensitivity \(\frac{dJ}{d\theta}\):
- In forward pass, \(\mathbf{\hat{u}}_1 = \text{ODESolve}(f_\theta, \mathbf{u}_0, t_0, t_1)\), where dynamic is specified by neural-network \(f_\theta\)
- Solve ODE terminal value problem specified by equation (15) for adjoint state \(\mathbf{a}(t)\)
- Compute sensitivity \(\frac{dJ}{d\theta}\)
Implementation
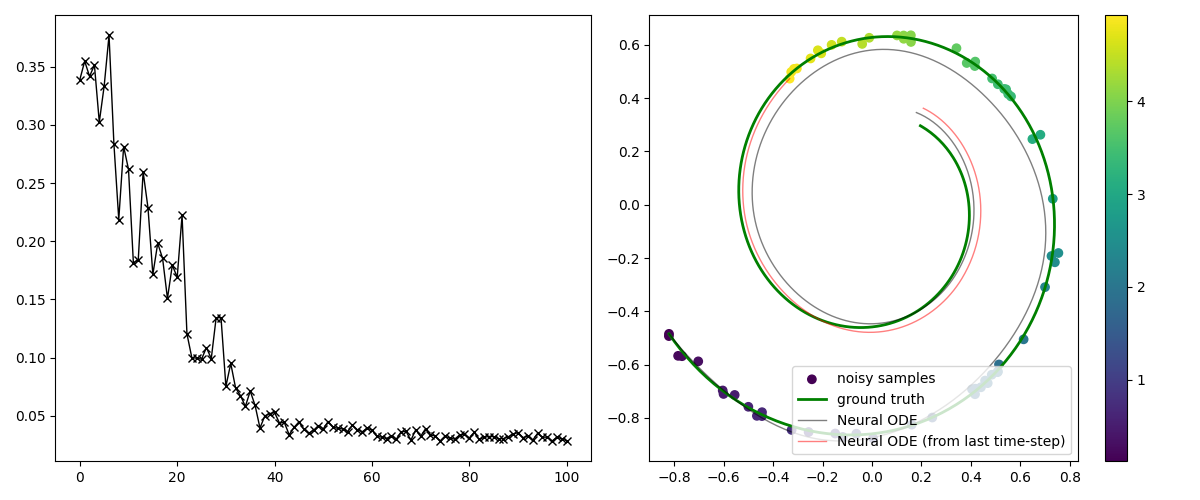
- Git to my version of implementation
References
- Patric Kridge’s thesis On Neural Differential Equation.
- Efficient gradient computation for dynamical models