Motivating example
Evaluating following integral
$$ I = \int_0^1{\frac{1 - x^2}{\ln{x}}dx} $$
Closed-form results
$$ \begin{equation} \begin{aligned} F(t) &= \int_0^1{\frac{1-x^t}{\ln(x)}dx} \\ \implies \frac{d}{dt}F &= \frac{d}{dt}\int_0^1{\frac{1-x^t}{\ln(x)}dx}\\ &= \int_0^1{ \frac{\partial}{\partial t} \frac{1-x^t}{\ln(x)}dx }\\ &= \int_0^1{ \frac{-\ln(x)x^t}{ln(x)} dx} \\ &= \bigg[-\frac{x^{t+1}}{t+1}\bigg]_0^1\\ &= -\frac{1}{t+1}\\ \implies F(t) &= -\ln({t+1}) \\ \implies I &= f(2) = -\ln3 \end{aligned} \end{equation} $$
Numerical approximation
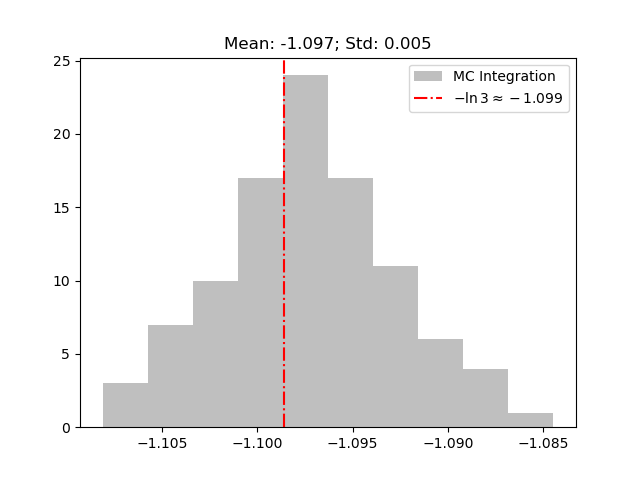
Code to produce the figure
1
2
3
4
5
6
7
8
import numpy as np
from matplotlib import pyplot as plt
def I():
g = lambda x: (1 - x**2)/np.log(x)
vG = np.vectorize(g)
x = np.random.uniform(0, 1, 10000)
return vG(x).mean()